Audio logarithmic measurement dB
Sound is transmitted as a disturbance in the air, within a certain frequency and energy range that humans can hear.
The loudness and strength of the sound that a person can hear are measured by the amount of pressure generated by the sound,
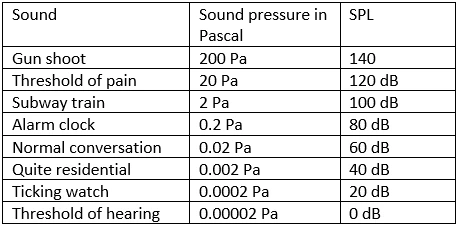
and this pressure is measured in the Pascal unit. A person can sense the sound starting from a low pressure of 0.00002 Pascal to
a high pressure of 200 Pascals at the middle frequency. It is difficult to express these values linearly and in the value of Pascal,
so the logarithmic system is used to express the audio power, making it easy to understand the least change in the input
and the corresponding output, as seen in audio amplifiers.
When it comes to sound measurement, the most commonly used logarithmic scale is the decibel (dB). A decibel is a unit of measurement
that expresses the ratio of two quantities, such as the ratio of a sound pressure level to a reference sound pressure level. It is a logarithmic scale,
which means that each increment on the scale represents a tenfold increase or decrease in the quantity being measured.
dBu dBV dB-SPL
The decibel scale is also useful for measuring sound levels in different contexts. For example,
dBu and dBV are special units of measurement used in audio engineering to express the voltage levels of
audio signals. dBu is a measurement of voltage relative to 0.775 volts, while dBV is a measurement of voltage
relative to 1 volt. To convert between these units, an increment of 2.21 dB must be added to dBu when converting to dBV..
Another important logarithmic scale used in sound measurement is dB-SPL, which stands for decibel sound pressure level.
This scale is used to measure the intensity of sound in the atmosphere and is particularly useful for measuring noise levels
in different environments. The reference point for dB-SPL is 0 dB, which is the threshold of human hearing at 1 kHz.
Calculation
To calculate the change in dB, the equation dB = 10log((power 2)/(power 1)) is used for power measurement. For other values,
the equation dB = 20log((value 2)/(value 1)) is used.
In conclusion, logarithmic scales are essential for accurately measuring and comparing sound levels. They provide a way to
express sound levels that are more in line with human perception and are widely used in audio engineering, acoustics,
and other fields. Understanding how to use and interpret logarithmic scales is essential for anyone working with sound.